확률 변수 X의 자연 로그가 정규 분포를 따를 때, 확률 변수 X는 로그정규분포(lognormal)를 따른다고 한다.
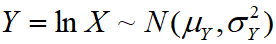
이 때 확률 변수 X의 확률 밀도 함수(PDF: Probability Density Function)나 누적 분포 함수(Cumulative Distribution Function)는 해당 확률 변수의 자연 로그 값인 Y의 평균과 분산을 매개변수로 정의된다. 이와 마찬가지로 로그정규분포와 관련한 MATLAB 함수에서도 Y의 평균과 표준편차 값을 넣는다.
이는 만약 로그정규분포를 따르는 data가 있다면 해당 data의 평균과 분산을 MATLAB 함수에 바로 넣어주면 안되고 로그를 취한 Y변수의 평균과 표준편차 값을 넣어야 한다는 의미이다. 확률 변수 X와 Y의 평균과 분산 간의 관계식은 아래와 같다.
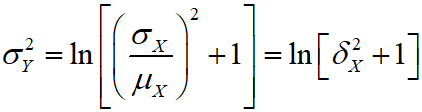
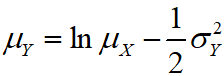
MATLAB에서는 이러한 변환을 해주는 함수도 존재하는데 lognstat이라는 함수다. 이 함수는 Y의 평균과 표준편차를 넣었을 때에 X의 평균과 분산을 반환한다.
기본 문법은 다음과 같다.
[mu_X, var_X] = lognstat(mu_Y, sig_Y)
예시를 통해 공식과 잘 상응하는지 확인해보자.
ex>
X = lognrnd(1, 1, [10000,1]); % Y의 평균과 표준 편차가 1인 로그정규분포를 따르는 난수 10000개 생성
muX = mean(X), stdX = std(X) % 생성된 난수의 평균과 표준편차 계산
covX = stdX/muX;
varY = log(covX^2 + 1), muY = log(muX)-0.5*varY % Y의 평균과 분산으로 변환 -> 각각 1에 가까운 값이 나오는 것 확인
[m, v] = lognstat(muY, sqrt(varY)); % lognstat을 이용하여 구한 Y의 평균과 분산으로 다시 X의 평균과 분산 도출
m, sqrt(v)
>> 이 코드를 돌리면 난수에서 계산한 X의 평균과 표준편차와 마지막 lognstat을 이용해 나타난 X의 평균과 표준편차(sqrt(v))의 값이 일치하는 것을 확인할 수 있다.
'MATLAB' 카테고리의 다른 글
| MATLAB 행렬에서 특정 열 벡터 또는 행 벡터 존재 여부 확인하기 (0) | 2021.05.24 |
|---|---|
| .mat 파일 저장 및 불러오기 (0) | 2021.05.04 |
| MATLAB 셀(cell) 배열 정의 및 호출하기, 관련 함수 정리 (0) | 2021.03.09 |
| polyfit, polyval 함수로 다항곡선 회귀분석하기(Polynomial Curve Fitting) (0) | 2021.02.07 |
| MATLAB의 particleswarm 함수로 최적화 문제 풀기(Particle Swarm Optimization) (0) | 2021.01.23 |