1. fmincon: Optimization 문제를 풀 때 사용하는 MATLAB 함수

2. MATLAB에서의 기본적인 설명
1) 기본 문법(syntax)
('help fmincon' 입력 시 나오는 내용)
fmincon - 제약 조건이 있는 비선형 다변수 함수의 최솟값 구하기
비선형 계획법 솔버입니다.
x = fmincon(fun,x0,A,b)
x = fmincon(fun,x0,A,b,Aeq,beq)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon)
x = fmincon(fun,x0,A,b,Aeq,beq,lb,ub,nonlcon,options)
x = fmincon(problem)
[x,fval] = fmincon(___)
[x,fval,exitflag,output] = fmincon(___)
[x,fval,exitflag,output,lambda,grad,hessian] = fmincon(___)
2) input 변수 설명
- fun: 목적함수 -> 함수 호출 방법을 따름: m파일을 정의한 문자열, 함수 핸들, 익명(Anonymous) 함수로 정의된 함수명 등
ex: 'CostFunc', fun = @CostFunc, fun = @(x) x(1)*x(2) + x(1) + 2*x(2) -6;
- x0: 초기값, 배열 형태로 정의 ex: x0 = [1, 1];
- A: 선형 부등식에서의 행렬
- b: 선형 부등식에서의 벡터
-> 즉, A*x≤b
- Aeq: 선형 방정식에서의 행렬
- beq: 선형 방정식에서의 벡터
-> 즉, Aeq*x=beq
- lb(lower bound): 벡터 x의 각 구성요소들의 최소값
- ub(upper bound): 벡터 x의 각 구성요소들의 최대값
ex: x = [x1, x2, x3]이고 0≤x1≤10, -1≤x2≤9, -10≤x3≤5이면, lb=[0, -1, -10], ub=[10, 9, 5]
- nonlcon: constraint 함수 -> 함수 호출 방법을 따름: m파일을 정의한 문자열, 함수 핸들, 익명(Anonymous) 함수로 정의된 함수명 등
ex: 'ConstFunc', fun = @ConstFunc, fun = @(x) x(1)*x(2) + x(1) + 2*x(2) -6;
- options: optimset 또는 optimoptions로 정의된 struct 구조체 배열
ex: options = optimset('LargeScale', 'off', 'GradObj', 'on', 'GradConstr', 'on', 'TolCon', 1e-8, 'TolX', 1e-8);
ex: options = optimoptions('Display', 'iter', 'Algorithm', 'sqp');
※ linear constraint가 없으면 A, b, Aeq, beq는 [ ]로 처리한다.
3) output 변수 설명
- x: 최적의 x값, optimum solution
- fval: optimum solution에서의 cost function(=object function)의 값
- exitflag: 종료 상황을 설명하는 값으로 해가 local minimum이면 1의 값을 가짐.
- output: iteration, stepsize, algorithm 등의 내용(최적화 과정에 대한 내용)을 담은 struct 구조체 배열
- lambda: optimum solution에서의 선형 방.부등식, 비선형 방.부등식, lower bound, upper bound의 정보를 담은 구조체 배열
- grad: optimum solution에서의 cost function의 기울기 행렬
- hessian: optimum solution에서의 cost function의 헤세 행렬(Hessian 행렬)
3. 목적함수를 정의하는 m파일 구성 예시
function [f, gf] = CostFunc(x)
f = x(1) + x(2) + x(3) % object function 정의
if nargout > 1
gf(1,1) = 1; %gf는 gradient of object function
gf(2,1) = 2;
gf(3,1) = 3;
end
※ nargout: 현재 실행 중인 함수를 호출 시 지정된 함수의 출력 인수 개수 -> 즉 위 예시에서는 gf의 값까지 출력 인수로 지정이 된 경우 gf값을 계산하도록 한다.
4. constraint 함수를 정의하는 m파일 구성 예시
-> nonlinear한 constraint의 경우 직접 m파일로 함수를 정의한 후 사용(linear한 constraint는 A, b, Aeq, beq 사용)
function [g, h, gg, gh] = Ex_const(x)
g(1) = x(1)^2 - x(2)^2; % nonlinear inequality constraint
g(2) = (x(1)+1)^2 + (x(2)-2)^2 + 1; % nonlinear inequality constraint
h = x(1)*x(2)-1; % nonlinear equality constraint
if nargout > 2
gg(1,1) = 2*x(1); % gradient of nonlinear inequality constraint -> gg(a, b) = ∂g(b)/∂x(a)
gg(2,1) = -2*x(2);
gg(1,2) = 2*(x(1)+1);
gg(2,2) = 2*(x(2)-2);
gh(1,1) = x(2); % gradient of nonlinear equality constraint
gh(2,1) = x(1);
end
예제1 - linear constraint 문제
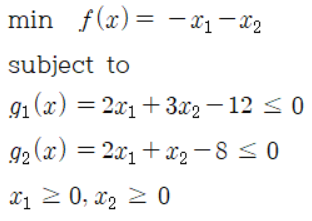
1-1. 목적 함수 정의
% ObjFunc.m file
function [f, gf] = ObjFunc(x)
x1 = x(1); x2 = x(2);
f = -x1-x2;
if nargout > 1
gf(1,1) = -1;
gf(2,1) = -1;
end
1-2. fmincon 사용하기
x0 = [0, 0];
fun = @ObjFunc;
A = [2, 3; 2, 1];
b = [12; 8];
Aeq = [];
beq = [];
lb = [0, 0];
ub = [inf, inf];
[x, fval] = fmincon(fun, x0, A, b, Aeq, beq, lb, ub)
예제2 - nonlinear constraint 문제

2-1. 목적 함수 정의
% ObjFunc.m file
function [f, gf] = ObjFunc(x)
f = x(1)*x(2); %Cost Func
if nargout > 1
gf(1,1) = x(2);
gf(2,1) = x(1);
end
2-2. constraint 함수 정의
% ConstFunc.m file
function [g, h, gg, gh] = ConstFunc(x)
g(1) = x(1)+x(2)^2;
g(2) = x(1)^2+x(2)^2-9;
h = [];
if nargout > 2
gg(1,1) = 1;
gg(2,1) = 2*x(2);
gg(1,2) = 2*x(1);
gg(2,2) = 2*x(2);
gh = [];
end
2-3. fmincon 사용하기
% Set bounds
Lb = []; Ub = [];
% Set initial design
x0 = [-1, -1]; % fmincon
[x, Funval, ExitFlag, Output, lambda, grad, hessian] = fmincon('ObjFunc', x0, [ ], [ ], [ ], [ ], Lb, Ub, 'ConstFunc')
'MATLAB' 카테고리의 다른 글
| MATLAB에서 csv 파일 및 txt 파일 읽고 쓰기 (0) | 2020.11.10 |
|---|---|
| MATLAB-Python 연결하는 방법 3 (2) | 2020.10.22 |
| MATLAB-Python 연결하는 방법 2 (0) | 2020.10.22 |
| MATLAB-Python 연결하는 방법 1 (0) | 2020.09.23 |
| 여러 확률분포들의 단일 변수 PDF 및 CDF 관련 MATLAB code (0) | 2020.06.05 |